Approximate Short Form - To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. An approximate identity (in the sense that you've described) is a sequence of operators, usually derived from some nice class, that. In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. Specifically, i know a is. I need to indicate an approximate inequality. Approximate $\int_0^\pi e^ {e^x} dx$ ask question asked 2 years, 10 months ago modified 2 years, 9 months ago
In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. I need to indicate an approximate inequality. An approximate identity (in the sense that you've described) is a sequence of operators, usually derived from some nice class, that. To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. Specifically, i know a is. Approximate $\int_0^\pi e^ {e^x} dx$ ask question asked 2 years, 10 months ago modified 2 years, 9 months ago
In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. Approximate $\int_0^\pi e^ {e^x} dx$ ask question asked 2 years, 10 months ago modified 2 years, 9 months ago Specifically, i know a is. To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. An approximate identity (in the sense that you've described) is a sequence of operators, usually derived from some nice class, that. I need to indicate an approximate inequality.
Linear Approximation Formula, Derivation, Examples
An approximate identity (in the sense that you've described) is a sequence of operators, usually derived from some nice class, that. Approximate $\int_0^\pi e^ {e^x} dx$ ask question asked 2 years, 10 months ago modified 2 years, 9 months ago Specifically, i know a is. In fairness, both the title and the statement 'i am wondering what is the best.
150 useful symbols and abbreviations for note taking Artofit
Specifically, i know a is. To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. I need to indicate an approximate inequality. An approximate identity (in the sense that you've described).
The Residual Zonal Flow in Toroidally Rotating Tokamak Plasmas ppt
In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. I need to indicate an approximate inequality. To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. An approximate identity (in the sense that you've described) is a sequence of operators,.
Linear Approximation and Differentials in Calculus HubPages
In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. I need to indicate an approximate inequality. Specifically, i know a is. To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. An approximate identity (in the sense that you've described).
Exact vs. Approximate Answers in Math (3column notes) YouTube
I need to indicate an approximate inequality. In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. Approximate $\int_0^\pi e^ {e^x} dx$ ask question asked 2 years, 10 months ago modified 2 years, 9 months ago An approximate identity (in the sense that you've.
depotqery Blog
An approximate identity (in the sense that you've described) is a sequence of operators, usually derived from some nice class, that. Approximate $\int_0^\pi e^ {e^x} dx$ ask question asked 2 years, 10 months ago modified 2 years, 9 months ago Specifically, i know a is. In fairness, both the title and the statement 'i am wondering what is the best.
What is Approximation How to find approximate value YouTube
To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. An approximate identity (in the sense that you've described) is a sequence of operators, usually derived from some nice class, that. In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more..
Business Email Short Forms Cheryl Hauck's Template
Specifically, i know a is. In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. Approximate $\int_0^\pi e^ {e^x} dx$ ask question asked 2 years, 10 months ago modified 2 years, 9 months ago I need to indicate an approximate inequality. To indicate approximate.
How to Approximate a Number ExamSolutions YouTube
To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. I need to indicate an approximate inequality. An approximate identity (in the sense that you've described) is a sequence of operators,.
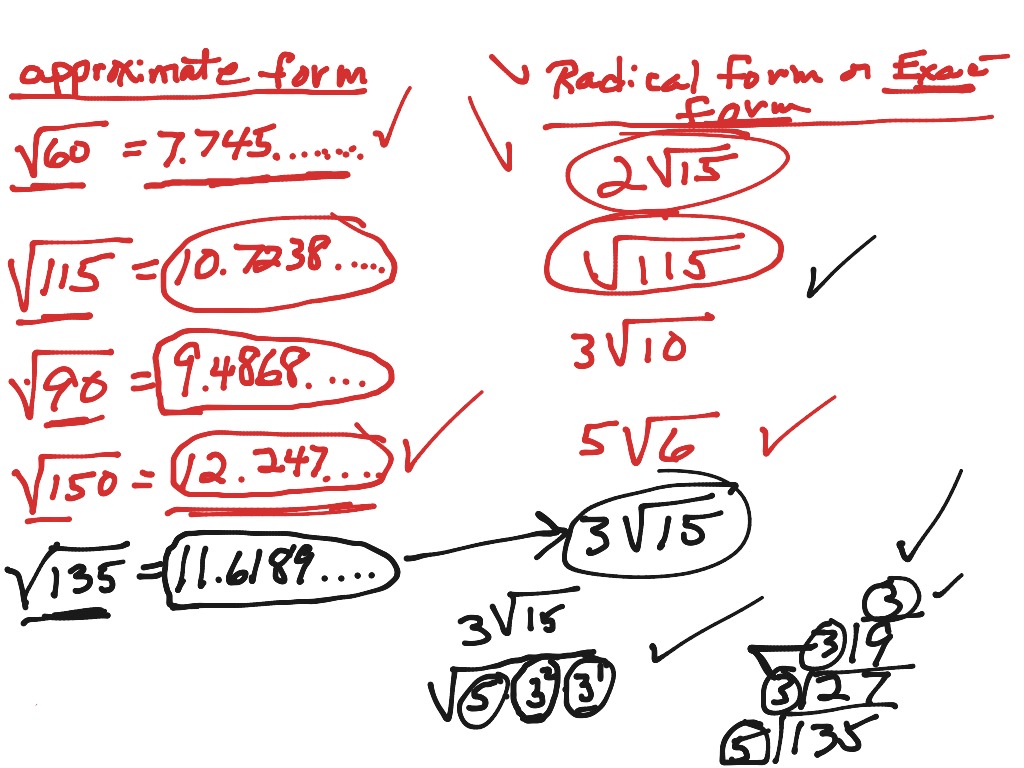
Radical & approximate form Math, Algebra 2 ShowMe
In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. Specifically, i know a is. To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. I need to indicate an approximate inequality. Approximate $\int_0^\pi e^ {e^x} dx$ ask question asked 2.
An Approximate Identity (In The Sense That You've Described) Is A Sequence Of Operators, Usually Derived From Some Nice Class, That.
To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. Approximate $\int_0^\pi e^ {e^x} dx$ ask question asked 2 years, 10 months ago modified 2 years, 9 months ago In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more. I need to indicate an approximate inequality.


+18.jpg)